Figure 1. The beginning of the ant and dot's paths.
To see a world in a grain of sand, / And a heaven in a wild flower, / Hold infinity in the palm of your hand, / And eternity in an hour.
—William Blake, Auguries of Innocence
ONE OF my favorite things to look at when I was a kid was my dad's globe. This was a National Geographic affair; it was not mounted, but instead sat freely in a clear plastic stand. It was also a quality item, and my dad made it clear to me that I was only to look and touch gently, not throw about like a ball.
I formed all sorts of weird ideas about the globe. It was one of my first exposures to the idea that we were not on top of the world. (I grew up in the Bay Area in California.) Instead, we were at a latitude of 40 degrees, and it occurred to me that we therefore did not stand up straight, when we thought we were standing up straight. Instead, we stood at an angle, of 50 degrees to the vertical. If we had really wanted to stand up straight, we should have leaned over by an angle of 50 degrees, toward the north. As I said, I formed all sorts of weird ideas about the globe.
The clear plastic stand, incidentally, had a number of fascinating symbols and etchings on it. There was a grid of squares, each covering 100 square miles on the globe. There were latitude and longitude markings, so one could see at an instant how far two different cities were displaced in those coordinates.
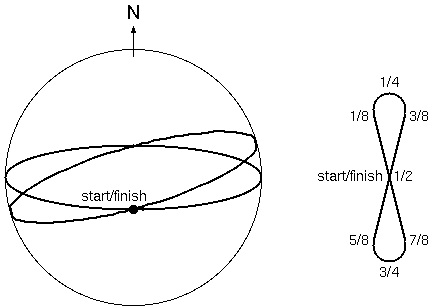
The thing that fascinated me most about the globe, however, was an unexplained, elongated figure-8 that was unceremoniously placed in the sparse expanse of the southeast Pacific. What was it, I wondered? It had the names of the months marked at various points around the curve, so it clearly had something to do with the year, but what was the significance? Why was it in the shape of a figure-8? What was it doing down there in the south Pacific? And couldn't people remember the months of the year without being reminded by a strange marking on a globe?
I'm sure you're dying to know the answers to those questions (well, maybe not the last one), so I'll give them to you, but let me start the usual way—with something that seems unrelated at first blush.
In his Republic, Plato (427–347 B.C.) describes—among a whole host of other things—his curriculum for the ideal schooling in the Republic. One of the subjects to be studied, as a science, is that of astronomy.
We must keep in mind, however, that Plato's conception of astronomy was not what we moderns are used to. The image that most people today have of astronomers is that of a solitary observer, dwarfed by a tremendous telescope, staring up at the sky in search of goodness only knows what. (As a matter of fact, most professional astronomers today rarely if ever look through the telescopes they use to do their research, but that's a development of the last century or so.) The job of the astronomer is to make observations of the heavens, and from those observations, enhance our knowledge of the cosmos.
That was most certainly not Plato's ideal. His curriculum was designed in order to form rigorous thinkers, and to that end, the "real" astronomy was not what was up in the sky. The stars and the planets showed inconsistencies that were a result of being sensible objects in the physical world. It would be no more appropriate to study the "real" astronomy by looking up at the sky than it would be to study geometry by looking at the imperfect straight lines and round circles that humans could draw out in the sand. Astronomy was a set of abstract concepts that could only be approached by logical thought. (He would surely have been distressed by Hipparchus's attempt to keep track of the changing heavens by mapping the stars.)
Accordingly, when Plato and his followers sought solutions to astronomical conundrums, the first criterion by which the solutions were measured was not how well they matched observations (although it was something of a consideration of Plato's), but by how elegant those solutions were. For example, Plato and his contemporaries felt that the most perfect shape was the circle. It is as perfectly symmetrical as any shape can be; it is, in a sense, the figure that all regular polygons aspire vainly to be. So, they concluded, the ideal astronomical theory for any problem must consist of circles or combinations of circles.
One such problem was the motions of the planets in the sky. The planets do not stay in place as the stars do, but instead move through the constellations. Mostly, they move slowly from west to east ("prograde" or "direct" motion) as the months pass, but occasionally, they move east to west ("retrograde" motion). Even such an idealist as Plato could not ignore that blatant a variation in motion. After all, the Sun and the Moon don't exhibit retrograde motion, so there was a clear basis for comparison. But Plato was no mathematician—he was an idea man, not an analytical genius. So he was forced to pose this question to others: What theory, consisting of circles, either in isolation or in combination, could explain the apparent motion of the planets?
Eventually, a workable solution was arrived at, centuries after Plato's death, by the Greek astronomer Ptolemy (c. 85–165), in his geocentric theory of the solar system. But long before Ptolemy, other Greeks tried their hand at solving Plato's poser. One such person was Eudoxus of Cnidus (c. 400–347 B.C.), a Greek mathematician and a contemporary of Plato.
Eudoxus's idea can be imagined as follows. Suppose that you have, resting on a tabletop, a globe that spins on a tilted axis (unlike my dad's free-standing globe). Imagine that there's an ant walking along the equator. Obviously, the ant retraces its path periodically, and we might call each time around the path one orbit.
Because the globe is tilted, the ant does not stay at the same height above the table throughout each orbit, but rather rises and falls. If at one point during its travels, the ant is at its lowest point, then half an orbit later (and half an orbit earlier as well), it is at its highest point. Midway between these extremes, the ant is at its average height.
Now, suppose that instead of putting the globe on a table, you put it on a turntable, and you set the turntable spinning at exactly the same rate as the ant's walking, but in the opposite direction. For example, if we assume that the ant is walking west to east along the equator—that is, counterclockwise, as seen from above the north pole—then the turntable is spinning clockwise. Then, because the two motions roughly cancel each other out, the ant appears to remain more or less in place (relative to an outside observer).
But not precisely in place. The ant would stay exactly in place if the globe weren't tilted, for then both the ant and the turntable would be moving horizontally, and their equal but opposite rotations would cancel each other out completely. But because the globe is tilted, the rotations don't cancel out perfectly, and the ant must at least be sometimes high, sometimes low. After all, without the turntable, the ant's height goes up and down, and the turntable can't affect the ant's height; it can only move the ant side to side.
Is that all? Does the ant only move up and down, or does it trace out a more complex figure? Now, to make that more precise, suppose you start the globe with the ant on the equator exactly at its average height, and you shine a laser pointer on the ant. (It's a weak pointer that doesn't hurt the ant.) As the turntable rotates clockwise, both the ant and the laser dot move west to east across the globe, but whereas the ant stays at the same latitude (0 degrees, on the equator), the laser dot appears to change latitude throughout its orbit. In fact, since the globe is tilted by 23.4 degrees—the tilt of the Earth's axis—the laser dot's latitude fluctuates between 23.4 degrees north and 23.4 degrees south. Now, the crucial question: Relative to the laser dot, what is the motion of the ant—or just as significantly, from the point of view of the ant, what is the motion of the laser dot?
Eudoxus had sufficient genius for visualization that he arrived at the surprising but right answer. Here's how he might have reasoned. If the Earth were flat, you could walk forever in a straight line without retracing any part of your path. But the Earth is not flat; instead, as Eudoxus probably suspected, it's a sphere. And since the sphere is curved, you can't walk a literally straight line. The curvature of the Earth forces your path to be curved one way or another. The straightest path you can walk is to go around the Earth in as wide a circle as possible. One such path is the equator; you can easily see that by walking along the equator, you are neither turning north nor south. Another way to walk as straight as possible is to start at the north pole, walk due south along some particular line of longitude until you get to the south pole, and then return to the north pole along the "opposite" line of longitude.
Each of these straightest paths is called a great circle. There are an infinite number of them on the Earth, or on the globe, or indeed on any sphere. Each of them has the same diameter as the sphere, and the center of any great circle is the same as the center of the sphere. The ant on the globe traces out a great circle—namely, the equator. The laser dot traces out another great circle, but one that is horizontal and therefore not the equator. Since the globe is tilted by 23.4 degrees, the laser dot's great circle is tilted to the equator by 23.4 degrees as well. These two circles intersect at two opposite points, which must obviously be along the equator, 180 degrees apart. This is the key to Eudoxus's idea.
Suppose we start with the ant and the laser dot at the same spot again. The ant proceeds directly eastward along the equator. The laser dot follows a great circle that is inclined to the equator, by 23.4 degrees, either to the northeast, or the southeast. For the sake of discussion, let's suppose that the laser dot is moving to the northeast of the original starting point.
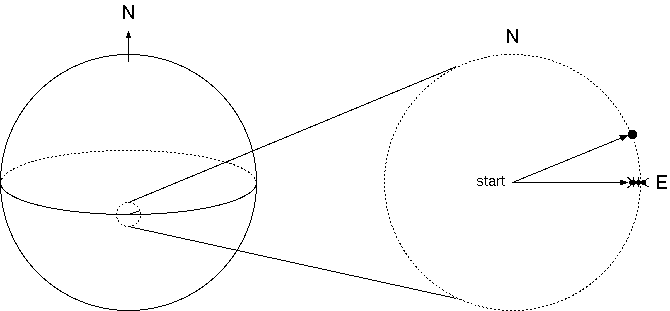
At first, the ant and the laser dot are still close together, and we can for all practical purposes ignore the spherical shape of the globe, just as, in real life, we can ignore the spherical shape of the Earth when navigating inside our home. Since the ant and the laser dot are moving at the same speed, they appear to be carried along at the edge of an ever-expanding compass dial, as in Figure 1.

Initially, the laser dot seems to be moving mostly northward, relative to the ant. But because the ant puts all of its motion into the eastward direction, and the laser dot only puts most of it there, the laser dot must also appear to be moving slightly westward, from the standpoint of the ant. (See Figure 2.)
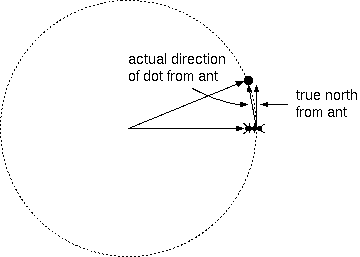
If the globe were actually flat, the ant and laser dot would spread out forever, with the dot always moving to the north-northwest of the ant. But the globe isn't flat, and if the ant and laser dot continue far enough, the globe's curvature will come into play.
For example, after a quarter of an orbit, the ant is 90 degrees (1/4 of 360) away from its starting point, along the equator. The laser dot, travelling at the same rate, is also 90 degrees from its starting point, but north of the ant. You might expect that it would also be somewhat to the west of the ant, as before, but it's not. Instead, it's exactly due north of the ant. (See Figure 3.)
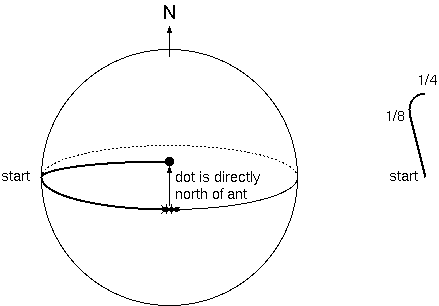
What has happened? The new factor is that the laser dot's path is taking it to higher latitudes on the globe, where the lines of longitude are closer together. As they both approach the 1/4-orbit point in their travels, therefore, the laser dot is gaining on the ant in longitude. This makes up perfectly for the start of their voyages, where the ant moved out ahead of the dot in longitude, so by the time that they have gone through a quarter orbit, both the laser dot and the ant have moved through exactly 90 degrees of longitude.
If we follow their motion further, into the second quarter of the orbits, the laser dot now races ahead of the ant in longitude. But we know that they must meet again after both have travelled through a half orbit; at that time, they must both be on the opposite side of the globe from their original starting point. As seen in Figure 4, from the point of view of the ant, the laser dot must have travelled in a wide looping path, starting toward the north-northwest, then curving eastward, then returning from the north-northeast.
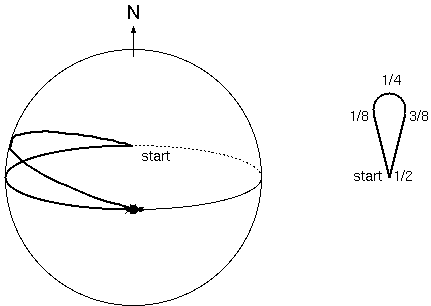
In the second half of their orbits, the exact same thing happens, except inverted. Again, the laser dot, with some of its motion toward the south, falls behind the ant in longitude, and it appears to the ant to be moving to the south-southwest. Then, as it moves to more southern latitudes, where the lines of longitude are closer together, it catches up with and overtakes the ant in longitude. Finally, as its path takes it back toward the equator, the ant and the laser dot meet once more at the starting point, one orbit later for each. (See Figure 5.)
This figure-8 shape is the path that the laser dot appears to take from the perspective of the ant. The amazing thing is that Eudoxus was able to figure this all out without the benefit of actual globes or laser pointers. To him, incidentally, the looping path, retracing itself over and over again, resembled the loops placed around a horse's feet to fetter it, so he called the path a "horsefetter." Naturally, he spoke Greek, so the word he used was hippopede, pronounced "hip-POP-puh-dee," from the Greek words for "horse" and "feet."
Eudoxus thought that by superimposing this figure-8 loop on a third, underlying west-to-east motion, he could simulate the retrograde motion of the planets. Half the time, the hippopede would also be moving west to east, so the combined motion would be west to east as well—this would be prograde, or direct, motion. Even much of the rest of the time, the hippopede would not be moving enough in the opposite direction to counteract the general west-to-east translation. Only when the hippopede was moving nearly as fast as possible, east to west, would there be a resulting backward slide, and this backward slide Eudoxus identified as retrograde motion.
It was a clever bit of explanation, but there were a number of problems with it. First of all, if it were correct, then all of the retrograde loops should have been symmetrical, and that wasn't so. Secondly, and more seriously, all the planets should remain at the same brightness throughout their orbits, and they certainly did not. Mars, in particular, is dozens of times brighter at some times than at others. For these reasons, Eudoxus's hippopede was eventually replaced, first by Ptolemy's theory of deferents and epicycles, equants and eccentrics, and 1,400 years thereafter by Copernicus and the heliocentric theory.
The hippopede re-entered science, though, in a completely unexpected way—a way that was only opened up by the advent of accurate timekeeping.
For millennia, humans kept track of time by noting the general location of the Sun. One might speak of leaving for town at sunrise, or of returning when the Sun was a hand's breadth above the horizon, and so forth. The Sun's motion was sufficiently constant to provide a convenient basis for telling time.
At some point, it became expedient to divide both the day and the night into portions, and the Babylonians chose to divide them both into 12 equal parts called "hours," from an ancient Greek word meaning "time of day." Twelve was a useful number, in that a quarter, or a third, or a half of a day or night all came out to a whole number of hours. These hours could be labelled on a sundial, so the moving shadow of a stylus, or gnomon, would mark out the advancing hours—at least, during the daytime.
Unfortunately, all of the daytime hours were equal to each other, and all of the nighttime hours were also equal, but the daytime hours were not the same length as the nighttime hours. Instead, they were longer in summer (naturally) and shorter in winter. The explanation for this was in the changing height of the Sun. It rose higher in the sky in summer, and more of its circular path was then above the horizon, so naturally the 12 daytime hours took longer to pass. In the winter, exactly the opposite was true: the Sun did not get very high at all in the sky, even at its peak. Less of its circular path was above the horizon, so the 12 daytime hours took less time to pass.
Eventually, other devices for telling time were developed that did not depend on the slightly variable nature of the Sun's path: for instance, hourglasses, or burning candles. With the introduction of these timekeepers, the variations in the daytime and nighttime hours became quite troublesome. It was tedious to have to change candles or hourglasses with each month. How much easier it would be to replace the inconstant hours with 24 equal ones. The only inconvenience was that sunrise and sunset would take place at slightly different hours throughout the year, but that could easily be accounted for.
Then, in 1656, the Dutch astronomer and physicist Christiaan Huygens (1629–1695) developed the first pendulum clock. Galileo had had the idea previously, while watching a chandelier sway back and forth in a cathedral, but had never followed through on a design. Huygens was the first to overcome the physical obstacles to building a clock based on the principle of the pendulum, and he ushered in the era of precision timekeeping.
Huygens's clock was also the first to be accurate to minutes a day, and the clock face gained another hand. Later clocks were even accurate to seconds, and now was discovered an interesting discrepancy. The moment that the Sun crosses the meridian—an imaginary north-south line in the sky—is called local noon, after an old word meaning the ninth (daytime) hour of the day. (This was midafternoon, but later was moved back earlier, to midday.) By all rights, the time between local noon on two successive days should be exactly 24 hours. But as measured by these accurate clocks, the interval between two consecutive local noons was sometimes a few seconds long; at others, a few seconds short. If we set a clock exactly to noon when the Sun was at local noon on one day, then the next day, the Sun would reach local noon, not at 12:00 exactly, but perhaps at 11:59:58, or at 12:00:10. These discrepancies added up, so that at various times of the year, the Sun was as much as a quarter of an hour "early" or "late." The errors repeated in a cycle of length one year, year after year.
Either the clocks were wrong, or the Sun's apparent motion across the sky was not as constant as previously thought (or both). We now know that it's the latter, and this repeating cycle is called "the equation of time" by astronomers. The Sun does not go at the same rate in right ascension (the astronomical version of longitude) all year long, but instead moves through lines of right ascension faster at some times, slower at others. At no point does it actually go the "wrong" way—it doesn't exhibit retrograde motion, in other words—but this variation is what causes the Sun to cross the meridian early or late. And if we plot the "location" of the Sun, with its northern and southern advances drawn along the vertical axis, and its earliness or lateness drawn along the horizontal axis, we get the figure drawn on my dad's globe, which is called an "analemma." (See Figure 6.)
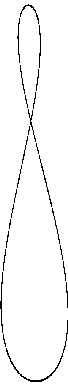
The word "analemma" is Greek for the pedestal of a sundial, and itself comes from the Greek verb analambanein, meaning "to take up, to resume, to repair," so that the pedestal is something that supports the sundial upon it. Early on, "analemma" seems to have been extended to refer to a particular kind of sundial, in which only the height of the Sun was indicated, by measuring the size of the shadow cast by the sundial. Later, it was used for a number of meanings related to the height of the Sun; its latest meaning, and that with which we are interested here, is some kind of representation of the Sun's gradually changing path in the sky at the same time (noon by the clocks) each day.
It surely hasn't escaped your attention that the analemma and Eudoxus's hippopede share a certain resemblance, a resemblance that, as it turns out, is more than accidental. The hippopede results from the conjunction of two circular motions, and so does the analemma.
The apparent motion of the Sun is really due to two motions of the Earth. One is the Earth's orbit around the Sun. The Earth completes one revolution about the Sun in one year, and if that were the only motion that the Earth had, then we on the Earth would see the Sun appear to go around the Earth just once a year.
However, the Earth has a second motion: its rotation on its axis. It does so approximately once a day, and it is for that reason, mostly, that the Sun appears to revolve around the Earth once each day. Since these two motions have periods in approximately the ratio 365.25:1 (the number of days in a year), while the hippopede results from two motions with equal periods, you might think that the hippopede doesn't have much relevance to the analemma.
But you'd be wrong. As I mentioned, the Earth rotates on its axis only approximately once a day, and the Sun's apparent motion across the sky is only mostly due to this rotation. A tiny component is due to the first motion of the Earth, its orbital revolution. Since this revolution takes 365.25 times longer than the rotation, it contributes 1/365.25 as much to the Sun's apparent motion across the sky as does the Earth's rotation. Now, the Earth's rotation makes the Sun seem to move east to west, from dawn to dusk, but its orbital revolution appears to add a second component, from west to east. This second component very slightly counteracts the first, so that the 24-hour day is longer than you might expect based solely on rotation. In fact, the Earth actually rotates on its axis, with respect to the stars, every 23 hours, 56 minutes, and 3.5 seconds. This slightly shorter day is called the "sidereal day," after a Latin word meaning "star," since this is the time it takes for the Earth to rotate once relative to the stars. The extra four minutes each day is due to the Earth's orbit around the Sun, and is 1/365.25 of the 24-hour day.
In other words, if the Earth didn't revolve around the Sun, but only rotated in place, in defiance of the law of gravity, the Sun would appear to go once around the Earth in 23 hours, 56 minutes, and 3.5 seconds, instead of the customary 24 hours. And if we were to take a snapshot of the Sun every day at the same time by the clock, it would be 3 minutes and 56.5 seconds further along each day. After two days, it would be ahead (that is, further west) by 7 minutes and 53 seconds; after three days, by 11 minutes and 49.5 seconds; after four days, by 15 minutes and 46 seconds, and so forth.
How long would it take for this margin to extend to 24 hours, so that the Sun would once again be "on time," on the meridian at noon? Why, as many times as 3 minutes and 56.5 seconds goes into 24 hours—and as we noted above, this interval is 1/365.25 of 24 hours, so it would take 365.25 days for the Sun to "lap" the 24-hour clock. A year, in other words. In short, if the Earth only rotated, and didn't revolve around the Sun, the Sun would appear to revolve around us every 23 hours, 56 minutes, and 3.5 seconds, but by taking snapshots of the Sun every 24 hours, which is just about four minutes longer, this motion would appear to be slowed down to just one revolution per year.
In case that sounds confusing, it's like watching a car drive by you on the road. In reality, the car's wheels may be rotating very rapidly—let's say, 25 times a second. (That'd be one fast car, by the way—probably around 150 to 200 kilometers an hour!) But if you watch a film of the car, where the camera takes 24 frames per second, each frame catches the wheel when it has gone through 1-1/24 of a rotation. Since the eye can't tell the difference between 1-1/24 of a rotation and just 1/24 of a rotation, it appears as though the wheel is actually rotating at only 1/24 rotation per frame. That works out to one rotation every 24 frames—or once a second.
In much the same way, when we take our figurative snapshots of the Sun every 24 hours, the Earth's rotation, alone, makes the Sun appear to revolve around the Earth, once a year, from east to west, along a path called the celestial equator. Meanwhile, as described above, the Earth's orbital revolution, alone, makes the Sun appear to revolve around the Earth, once a year in the opposite direction, from west to east, along another path called the ecliptic. Both the celestial equator and the ecliptic are great circles. What's more, these two great circles are not the same, but because of the Earth's axial tilt, are instead inclined to one another by an angle of 23.4 degrees.
We therefore have an exact analogue of Eudoxus's hippopede, but this time applied to the apparent motion of the Sun throughout the year. These two motions combine to create the figure-8 shape of the analemma. Eudoxus could not possibly have known about this application of his theory, which was originally designed to account for the retrograde motion of the planets. As an explanation of that behavior, the hippopede was basically dead on arrival. Too bad that accurate clocks were not available in his day; otherwise, he might have found the right use for his geometric intuition.
But one last objection remains: The analemma on the globe is not a symmetric figure-8 at all! Rather, it's smaller on the northern end, and larger on the southern end. Why is that?
That asymmetry is due to one further property of the Earth's orbit around the Sun: its eccentricity. The Earth's orbit is nearly circular, but not precisely so. It is actually an ellipse, and the Earth moves along that ellipse in accordance to Kepler's laws of planetary motion. (See "Music of the Ellipses.") As such, the Earth moves faster when it is closer to the Sun, and slower when it is further from the Sun, and this translates to a corresponding variation in the Sun's apparent west-to-east motion due to the Earth's revolution. Just how elliptical the orbit is, and the angle between the long axis of the orbit and the axis of the Earth, determine the contour of the analemma.
Incidentally, I'm not certain just why the analemma is specifically in the southern Pacific—perhaps because that's the least crowded part of the planet, cartographically speaking—or why it's needed on a globe at all. It does have some significance to sundial builders, since it can be used to correct for the equation of time, if the months of the year are marked out (as they are on my dad's globe) and one rotates the dial of the sundial according to the analemma. But it doesn't seem to need to be on a globe, and indeed, more modern globes now eschew the analemma in favor of a more extensive legend.
Here is a C program to compute and plot the analemma for various different orbital parameters. It's not tremendously user friendly, and can probably use some additional documentation. (It also uses the "system" call, which probably should be replaced with something in the "exec" family, if that means anything to you.) However, it uses the ideas presented in this essay, with the additional amendment that the eastward march due to the Earth's orbital revolution varies in speed because that orbit is elliptical. This approach is more accurate than programs where the effects on the equation of time of the two motions is added linearly (see, for example, http://www.analemma.com/). That's reasonably accurate for small eccentricities and axial inclinations, but becomes noticeably inaccurate for extreme orbits.
Copyright (c) 2002 Brian Tung