
Figure 1. Two eyes (L, R) and a coffee mug (M).
All I ask is a tall ship, / And a star to steer her by.
—John Masefield, Sea Fever
THE FIRST time I went to the airport on a business trip, I decided to take a taxi. I had a car, but I would be gone for several days and it would have cost more to park the car at or near the airport than it would to take the taxi. Besides, in the taxi, I reasoned, I could relax for a bit, maybe take a nap. (The flight left at six in the morning.)
Predictably, though, the cabbie was new at this, having just arrived in Los Angeles in the previous week, and clearly had his troubles finding his way to the airport, conceivably the commonest destination for all of his fares. I had scarcely settled into my seat when the cab headed for the wrong transition ramp.
"No, this lane heads north," I explained in a rush, "you want that one that heads south. They criss-cross," I added, gesturing uselessly behind him. But he got the message. Nevertheless, the rest of the trip to the airport was an adventure as we nearly headed the wrong way a half-dozen times. After we finally arrived, I advised him to get familiar in a hurry with at least the principal landmarks in the L.A. area—admittedly a tough task with the expanse of it—before he got laid into by a commuter with a tighter schedule.
Still, I've made my mind up: No more taxis for me. L.A. is not a taxi town, anyway, and it is less hassle to drive and have to navigate for myself than it is to be in a taxi with the expectation of not having to navigate, and then end up directing the way just the same.
In the sky, too, people have been navigating their own way since before there were telescopes. With the unaided eye, this wasn't so hard, since over the generations people began to pick out noticeable patterns in the stars, and the sky is not so large in any case that it can't be apprehended after a year or so of acquaintance. Moreover, we're used to moving our head this way and that—with the horizon essentially in constant view, it's hard to lose your way.
But not so with the telescope! The telescope has a much narrower field of view than the unaided eye; the eye has about a 180 degree wide field, more or less, so that it is basically possible to maintain the entire sky in view if you lie on the ground and look straight up. A telescope at even low powers, on the other hand, has a field of view perhaps a couple of degrees wide. A paper towel tube is perhaps a foot long and two inches in diameter. Imagine looking only through the tube with one eye and trying to find your way to any given object in the sky. Even with a comprehensive knowledge of the stars it would be very difficult to land on your destination. And that paper towel tube actually has a field of view about 10 degrees wide, much wider than any conventional telescope. Looking through a telescope at moderate powers is really more like looking through a soda straw.
For this reason, few people navigate their way solely through the telescope. A variety of techniques and mechanisms have been developed to help point a telescope in the right direction to find objects, from sighting along the tube at a point in space, to gunsights, to finderscopes, to unit-power reflex finders like the popular Telrad, to finder circles. But arguably none has had the impact that two electronic navigation tools have had: digital setting circles (DSCs) and GOTO. In this month's column, we'll examine how these work. GOTO is in principle just a set of DSCs plus a device that automatically reads the DSCs and moves the scope, so there is in reality just one basic principle that guides both of these.
The first truly mass-produced "computerized" telescope was Celestron's Compustar. It was equipped with GOTO, meaning that one could punch in the coordinates of an object, and the motor would automatically swing the scope toward the right spot in the sky. It could be calibrated using only a single alignment star. However, the Compustar had to be very carefully polar-aligned; the polar axis of the Compustar's mount had to be pointed precisely at the celestial pole, which in the northern hemisphere is less than a degree from Polaris. (See "Planning the Stars" for more information.) Any errors in alignment would propagate and magnify errors in pointing. This and the higher cost of the Compustar led (among other factors) to its eventual demise.
DSCs really work on a different principle altogether. With DSCs, the scope need not be aligned at all! DSCs can work even on alt-azimuth mounts, in which the telescope simply moves up and down and side-to-side. What's more, the initialization procedure for DSCs (and GOTO) is very simple—one need only point the scope at two different stars, as selected by the user from a list provided with the scope, and thereafter, the device is able to guide you to any celestial coordinates whatsoever. It can be said without undue exaggeration that the simplicity of using DSCs and GOTO (not to mention the sheer attraction of complex gadgets) has done more to draw in participants to the hobby than any other single invention since the telescope itself.
At first, the two-star alignment seems a miracle. How is it possible that locating two points in the sky could permit you to find any other celestial object? In fact, the method behind two-star alignment is quite simple. It's related to the way we locate objects with our own eyes.
In "Double Vision", I discussed the manner in which parallax allows us to determine the distance to objects. For example, when I view a nearby object (say, a coffee mug on a table in front of me), my two eyes see the coffee mug in slightly different locations. My left eye sees it as slightly to the right of where my right eye sees it, because it views it from a somewhat different angle. This is caused by the separation between my eyes. The different angles at which my eyes see the coffee mug is used by my brain to determine absolutely where the mug is, because one principle in geometry is that two known angles and a known side between them is sufficient to "fix" a triangle:

This is known as the ASA (for angle-side-angle) theorem. My brain knows geometry! (Yours does too.) The angles at my left eye (L) and my right eye (R) are known, as is the side length (LR), which is the separation between my eyes. This completely determines the triangle MLR, so that the location of the mug at M can be known with certainty, in turn allowing me to pick up the coffee mug without spilling its contents all over the table and floor. Now I am not aware of performing any geometry explicitly in my head, and yet I can direct my hand to reach for the mug without any problem at all; even two-year-olds can do this "GOTO" tolerably well. It's trained into our brains at a very early age.
Now, let's suppose that instead of eyes, we instead had two sonar devices on our heads, left (L) and right (R). These sonar devices can't "see" the objects in front of them, but they can send pings off of them and determine how far away there are. Again, because my sonar devices are separated, my left sonar will sense that an object is at a slightly different distance than my right sonar does. This too can be used to absolutely locate the coffee mug, because there is another theorem in geometry which says that three known sides is also sufficient to fix a triangle. This is known as the SSS (for side-side-side) theorem. Bat brains know geometry! In this case, we also need to know that the coffee mug is resting on the table in front of me. Otherwise, there are an infinite places that the coffee mug could be—for instance, it could be floating in mid-air in front of me.
We can use the SSS method for DSCs and GOTO as well, as it turns out. In this case, the mug can be assumed to be on the coffee table: we can view the sky as being a spherical sheet completely encircling the earth. The stars and other objects have distance, of course, as I described in "Double Vision", but it doesn't matter at all whether a star is 10 light-years away or 1,000; the telescope need not be pointed any differently in either case. This simplifies the alignment process.
Let's suppose that we choose Polaris and Procyon (the bright star in Canis Minor, the Little Dog) as our alignment stars. We want to use those stars to find M1, the Crab Nebula, which is too dim to see by the unaided eye. We look at our map, and we see that the distance between Polaris and Procyon is so far, between Polaris and M1 is so far again, and between Procyon and M1 is so far yet again. We've determined the three sides of our Po-Pr-M1 triangle, which according to the SSS theorem should be sufficient to locate M1.
When we get out under the skies to find M1, we immediately encounter a slight problem. On a map, of course, it's easy to find the distance between Polaris and Procyon, for example. In the sky, however, we can't say that they're five inches apart, or five feet apart, or whatever; it depends on where we put our yardstick. It could be five hundred yards if we were to stick a suitably long stick behind an airplane. Absolute measures of linear distance have no meaning on the sky. We instead have to use a measurement called angular separation. Instead of saying that Polaris and Procyon are such and such a distance apart, we say that they are separated by an angle, which in this case is about 85 degrees. That means that if I extend one arm toward Polaris, and the other arm toward Procyon, my two arms make an 85-degree angle. Likewise, Polaris and M1 are separated by about 67 degrees, and Procyon and M1 are separated by just 28 degrees.
Our second problem is that the SSS theorem only works for flat, Euclidean geometries, such as the surface of a coffee table. We don't necessarily know that it works for elliptical geometries like the imagined surface of the sky. Does it? It can in fact be rigorously proved that it also works for the sky, provided that the points and triangles are defined properly.
There are some dangers. The two alignment stars can't be very close together, for one. If they were very close together, than the separations between either one of them and the target object would be very similar, and that would be true for a lot of positions. For example, if we chose as our alignment stars Polaris and Polaris's binary companion, then the separation between either one of them and M1 would be 67 degrees. We'd be able to tell that M1 was 67 degrees away from Polaris, but we wouldn't know which direction. (It could be anywhere along the circle of +23 degrees declination.) It would be like trying to figure out how far the moon is using the unaided eye. Our eyes are just too close to do the job.
The two alignment stars also can't be too far apart. The ultimate case, of course, would be two stars that were precisely on opposite sides of the celestial globe, 180 degrees apart. With two alignment stars that far apart, the two angular separations between our alignment stars and the target object always have to add up to 180 degrees. Again, there would be a whole circle of locations where our target could be, with no way to tell which was the right one.
Aside: This is one justification for the definition of the term "point" in elliptical geometry. In elliptical geometry, one way to define a "point" is as a pair of ordinary points on a sphere, diametrically opposite from one another. Therefore, a pair of stars opposite one another on the celestial globe would really be one and the same point.
The ideal separation is halfway in between, 90 degrees apart, so Polaris and Procyon make a nice pair of alignment stars. The elliptical version of SSS tells us that if we have the angular separations between Polaris and M1, and between Procyon and M1, there are two and no more than two places where M1 can be found. Why two? Because the geometry demands it. In the case of the coffee mug on the table, there are also two places where the coffee mug could be. One is at the location M as before, but there is also one potential place for the coffee mug—behind us at M', as in Figure 2 below:
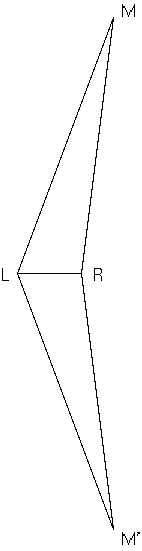
M and M' are mirror images of each other, reflected across the line joining L and R. So we have ML = M'L, and MR = M'R. In other words, M and M' are indistinguishable from each other, so long as we restrict ourselves to the distances of L and R to either of them. Some other way must be found to distinguish between them. This mirror-image kind of symmetry can be very troublesome in general in science. In our case, though, there's a very simple solution. If we were giving directions to the coffee mug at M, we would say, for example: Start at L. Proceed to R, and make a left turn to M. There is no way to go from L to R and make a right turn to M—one must make a left turn there. Similarly, you have to make a right turn in order to get to M'.
In the celestial, elliptical geometry world, there are also two places for M1. We can label them M1 and M'1. Either of them is 67 degrees from Polaris and 28 degrees from Procyon. However, if you proceed from Polaris to Procyon and make a right turn, you'll get to one of them, and if you turn to the left, you'll get to the other. In our case, a right turn leads to M'1, and a left turn leads to our true quarry: M1.
Aside: There is a way to express this in mathematics. If we let vPo, vPr, and vM1 represent the vectors from the observer (us) to Polaris, Procyon, and M1, respectively, then we can write
whereas with the faux M'1, we have
So long as we make sure which way the inequality goes for the actual object on our map, we can make the same turn in the sky.
Are we done yet? Not quite: Unfortunately—or fortunately, depending on your point of view—the stars and the rest of the universe appear to rotate around the earth once in a little less than 24 hours. This means that even an hour after our initial alignment, Polaris is of course fairly close to where it was initially, but Procyon has moved on about 15 degrees. If we use the old position of Procyon, we'll get an old location for M1. DSCs and GOTO must therefore institute a time correction. One way is to figure out where Procyon has moved to, and start over from the new location.
However, there's a short cut that we can take. Consider the location of M1 at the new time, one hour after alignment. What was the object that was there one hour earlier, at the moment of alignment? There may not have been an actual object there, but let's make an imaginary one up, called I1. This imaginary object I1 has the same celestial coordinates as M1, but shifted over by one hour (of right ascension). So, in order to find the location of M1 one hour after alignment, we simply look for where the object I1 would have been right upon alignment. That way, we can use the old locations of Polaris and Procyon.
Aside: This only works, incidentally, if the scope is non-driven, like non-GOTO alt-azimuth scopes and some equatorially mounted ones. If it's driven (and the scope has driven setting circles too), then you have to do one extra step: you have to move the scope back up by one hour of right ascension (or however long it has been since alignment).
That's essentially the story of two-star alignment—or at least, one way to do two-star alignment. There are others, which I won't go into in great detail in this column, because the mathematics becomes a bit more involved. One requires you to derive a matrix that models the rotation between the scope's axes of rotation and the sky's. You push the celestial coordinates you want in one side of the matrix, and—brrrappp!—out come the location in terms of the scope's mount on the other side, like one of those computers in '60s movies and TV shows.
Some alignment routines make use of just one star, but require you to level the scope accurately and punch in the time and location. Still other routines make use of three stars, so that they can account for problems such as mount flexure, or non-perpendicularity of axes. Still, the workhorse of DSCs and GOTO is two-star alignment, and as you can see here, it's not immensely complicated, once you get the hang of it.
As part of my work on the C5+, I developed code based on the method presented above to emulate DSCs for the C5+, which is a 5-inch Schmidt-Cassegrain telescope on a driven mount (the analog circles are driven as well). This code is called goto.c—an unfortunate misnomer, I'll admit—and can be found here. If you like, try it out. To make it work for an undriven mount, one need only modify the section that performs the time correction. There is also a small correction section for mount flexure and/or inaccurate measurement, but it's purely heuristic and has no theoretical basis.
One last thought: DSCs and GOTO mounts/telescopes typically promise pointing accuracy as tight as an arcminute or so. Ordinarily, these use optical encoders with a granularity of a few thousand, which still leaves 5 or 6 arcminutes between each step. How then do they achieve such tight precision? I can't say for sure, but I suspect that the detectors are capable of interpolating a position between two encoder steps, either by having a physically wide detector capable of spanning the space between two steps, or by determining the speed with which the encoders are being tripped. If you have better knowledge about this, please send me e-mail at <brian.y.tung@gmail.com> and share what you know.
In my February Column, Ten Myths, Myth Number Eight reads, "Light pollution filters are designed to block out light pollution." David Knisely wrote to point out that certainly some filters, such as the broadband filters, are designed to block out light pollution primarily—there is a deep valley in the transmission curve for sodium lights, for example. Generally, the other filters are not typically called LPR filters, although I point out that Orion calls both its broadband and narrowband filters LPR filters, and Orion is a big seller to beginners.
Copyright (c) 2000 Brian Tung